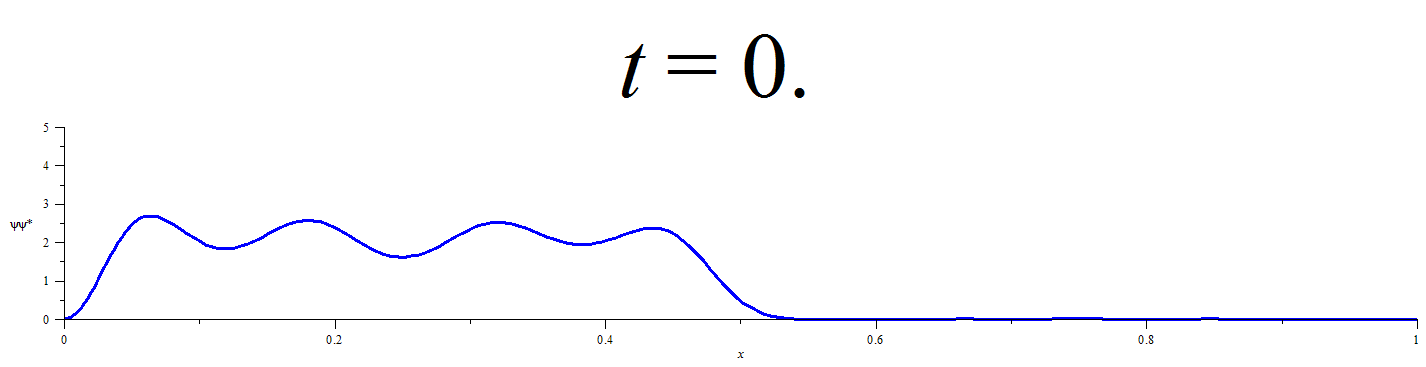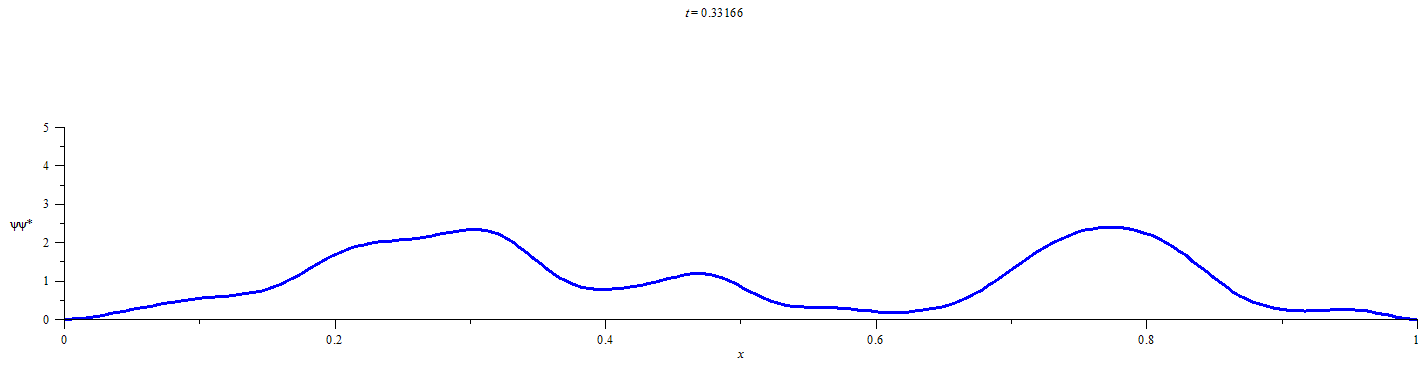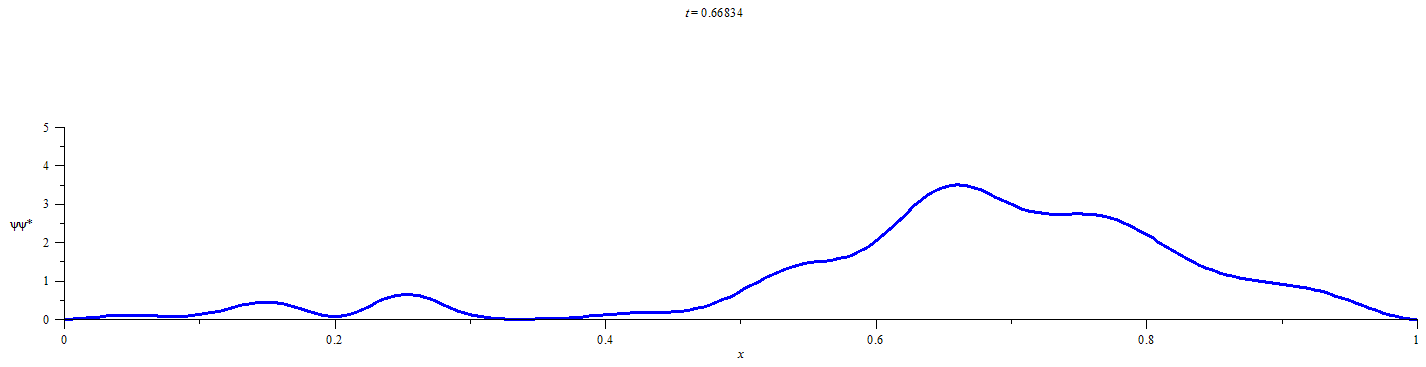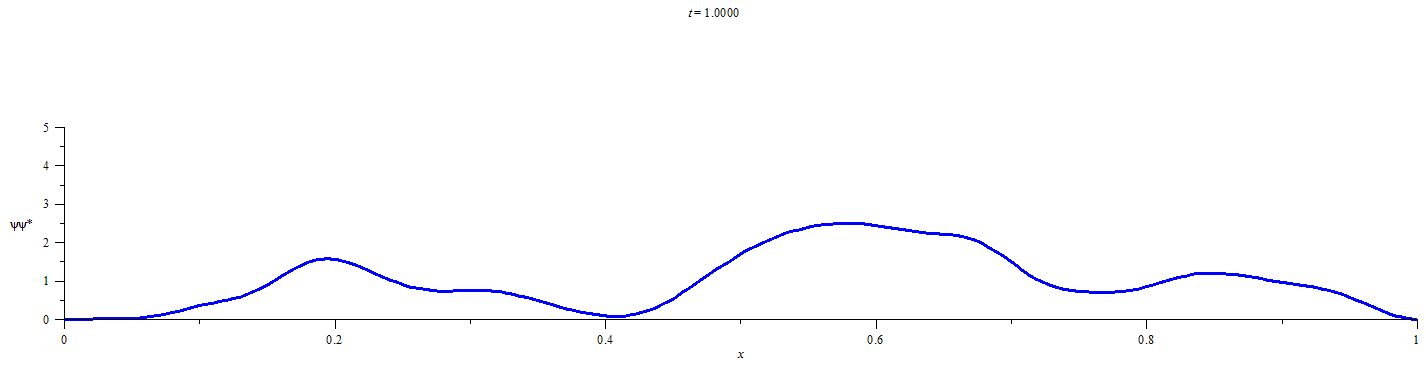
A Statistical Approach for Quantifying Quantum Particle Transit
The timescale of quantum particle movement has implications for biological charge transfer, chemical reactions, conductive materials, and nanoscale devices. It follows that knowledge of the timescale of quantum particle movement is important to the understanding of naturally occurring nanoscale systems, and for designing artificial ones. As a consequence of the uncertainty principle, the exact transit time for a quantum particle cannot be specified with arbitrary precision. Instead it is possible to answer, “How many discrete time-steps N of length ∆t must elapse before a quantum particle initially localized in region A has traveled to region B with a given probabilistic confidence?”
This statistical method requires obtaining a discrete representation of the time-dependent wavefunction for an initially localized quantum particle by numerical solution of the time dependent Schrödinger equation. Time propagation of the wavefunction followed by integration of the square modulus of the wavefunction over the limits of each defined spatial region at discrete time-points yields the extent of the probability distribution in each of the spatial regions. Conditional probability analysis is then applied to the M spatial-region occupancy probabilities by calculating the elements of an M x M “transition matrix” for each discrete time-step. The number of time-steps that must elapse before a chosen probabilistic confidence is recovered that a chosen spatial region has participated in the flow of probability density is then be calculated from the elements of the transition matrix at each time-step and the occupancy probabilities at t=0.
To learn more about this method, see our publication here.
Curtin, E., Bazargan, G., & Sohlberg, K. (2018). Quantifying electron transit in donor-bridge-acceptor systems using probabilistic confidence. Journal of Theoretical and Computational Chemistry,17(07), 1850046.
Quantifying the Timescale of Proton Transfer
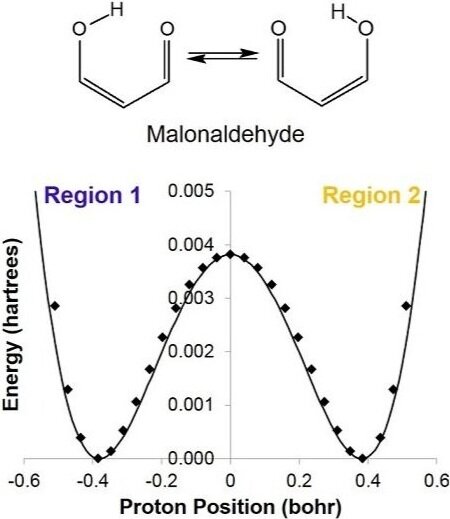
Proton transfer is a key step in many acid-base, enzymatic, and tautomeric reactions. Due to the ubiquity of proton transfer in chemical reactions, quantifying the timescale on which it occurs is essential to gaining a full understanding of chemical kinetics. For example, many simple compounds including β‑diketones, ɣ-diketones, and naphthazarins interconvert between tautomers through an intramolecular proton transfer between two oxygen atoms. In such cases, proton transfer occurs over a short distance along a hydrogen bond, typically on a short timescale.
Proton transfer times in a set of diketone compounds (in their enol forms) were quantified using the probabilistic approach. For each compound, a set of structures along the proton transfer path was generated by linear interpolation between the initial and transition state structures for potential energy curve (PEC) mapping. Each structure was subjected to a constrained optimization using electronic structure calculations based on DFT. The data were fit to a double-well potential.
The proton transfer times were quantified using the statistical approach and are found to be consistent with experimental estimates of proton transfer times in dicarbonyl compounds. Given that the height and width of the proton transfer barrier is similar for these systems, the predicted transfer times are on the same order of magnitude. Capturing the correct length and energy scales in the transfer potentials yields within an order of magnitude agreement between the statistical predictions of proton transfer times obtained from a one-dimensional model, and transfer times deduced from experimental observables. These results demonstrate the viability of the method as a tool for gaining insight into the kinetics of chemical reactions involving proton transfer.
To learn more about quantifying proton transfer, see our publication here.
Bazargan, G., Curtin, C., & Sohlberg, K. (2019). Comparing statistical predictions of quantum particle transit times in molecular systems to experimental measurements. Journal of Theoretical and Computational Chemistry,18(08), 1950039.
Quantifying the Timescale of Electron Transfer
Electron transfer times in a set of five donor-bridge-acceptor (DBA) molecules based on a tetracene donor, pyromellitimide acceptor, and p-phenylenevinylene oligomer bridges, were quantified. The energies of the molecular orbitals (MOs) relevant to the charge transfer process were extracted from DFT calculations, and plots of the corresponding MOs were visually inspected to determine the regions of the molecule on which they are localized.
An effective one-dimensional piecewise charge transfer potential was optimized for each DBA system. The difference between the relevant DFT-predicted MO energies and the eigenenergies calculated by solution of the time-independent Schrödinger equation for the one-dimensional potential, was minimized (Nelder-Mead simplex algorithm). After fitting an effective charge transfer potential for each DBA system, the electron transfer times were quantified using the statistical approach.
The electron was initially localized in the deeper well (donor region). The time evolution of the localized wavefunction was followed and subjected to conditional probability analysis. The overall trend in transfer times predicted using this approach is in qualitative agreement with the experimentally reported trend in transfer times for three choices of initial state and several difference metrics of transit time. The predicted length dependence of transfer times from the donor to the acceptor within this set of systems supports the experimentally inferred change in electron transfer mechanism from superexchange at short bridge lengths to hopping at long bridge lengths as a consequence of energy-matching between the virtual states of the donor and bridge. Signatures of both mechanisms can be found by inspection of the spatial region occupancy probabilities. These results show that this statistical approach can be used as a tool for quantifying electronic charge transfer.